Алгоритм раскраски графа c
Вы точно человек?
В этой записи я решил представить алгоритм, придуманный мной под впечатлением от распределённых distributed алгоритмов. Алгоритм строит субоптимальную правильную вершинную раскраску неориентированного графа. Алгоритм довольно прост и, возможно, был в том или ином виде представлен в литературе.




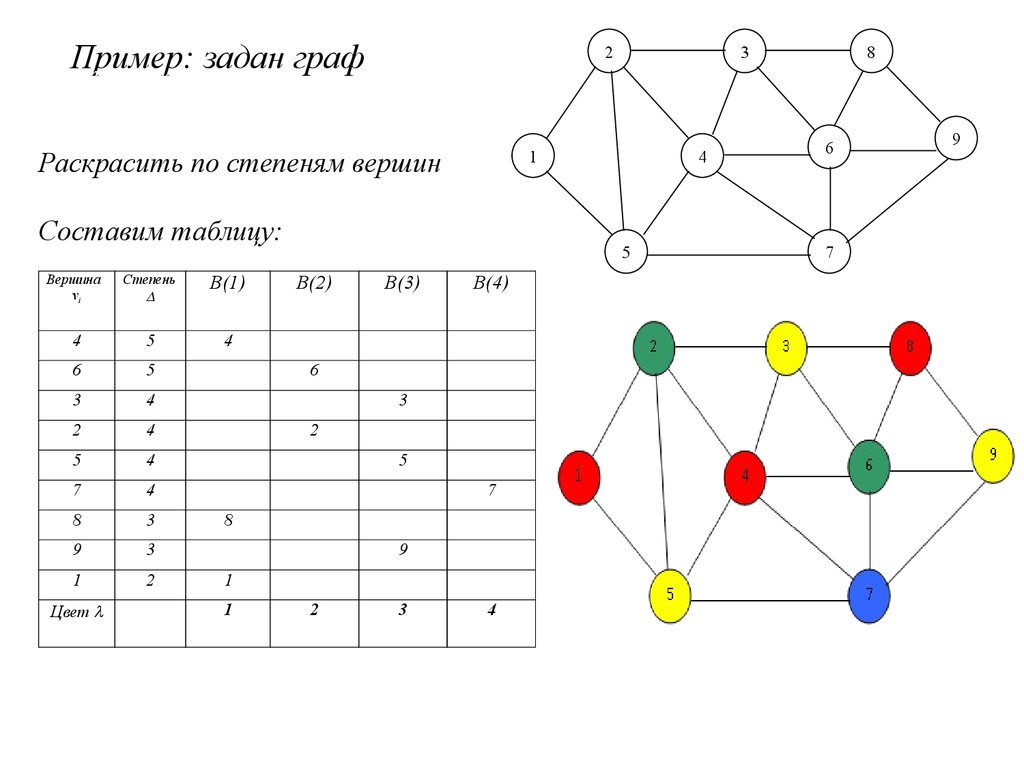
На этом шаге мы рассмотрим алгоритмы закраски графа. Задачи определения хроматического числа и построения минимальной раскраски произвольного графа являются очень сложными. С одной стороны, не известны алгоритмы их решения, сложность которых есть некоторая фиксированная степень от длины записи условий задачи так называемые полиномиальные алгоритмы.
- Алгоритм выделения компонент связности обыкновенного графа
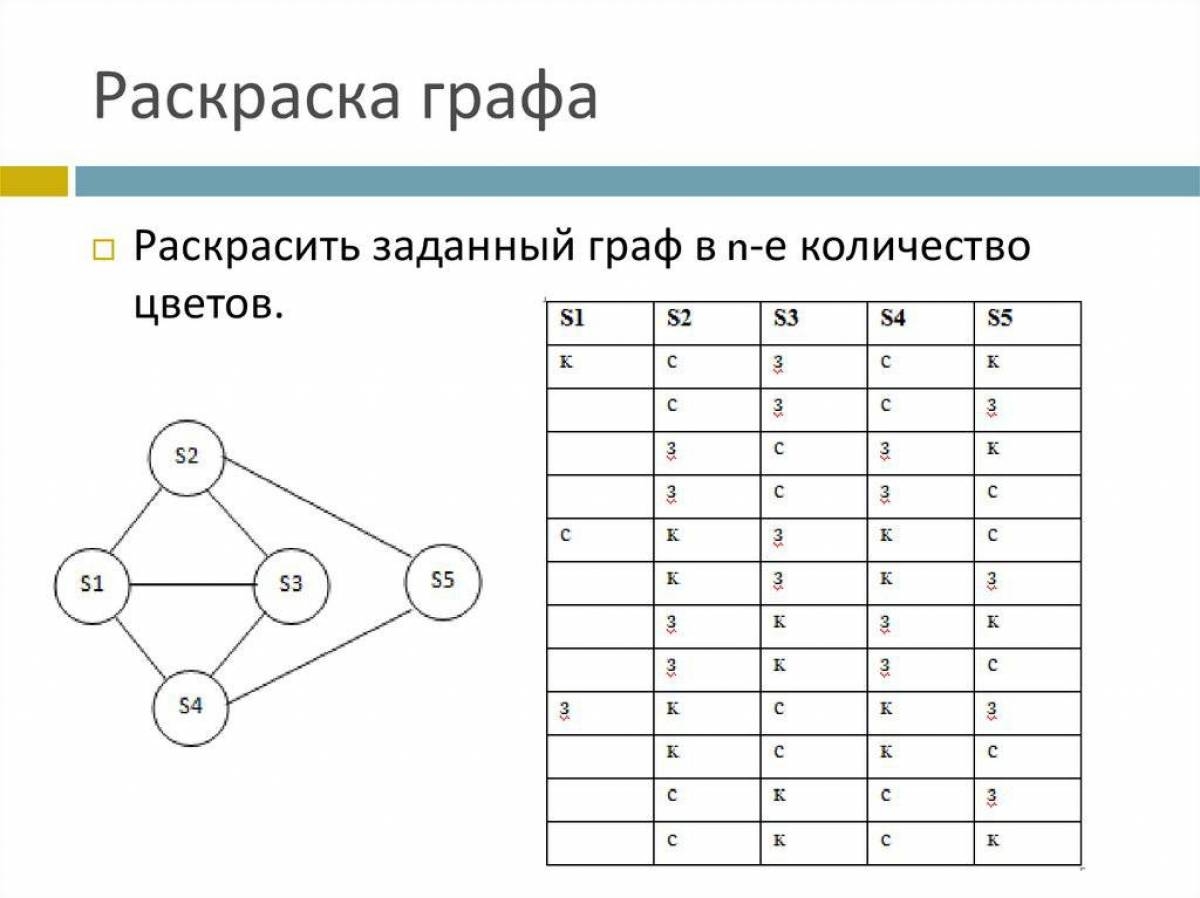
- Алгоритм раскраски графа позволяет находить точное или приближенное значение хроматического числа произвольного графа и соответствующую этому значению раскраску вершин. Граф G называют r-хроматическим, если его вершины могут быть раскрашены с использованием r цветов красок так, что не найдется двух смежных вершин одного цвета.
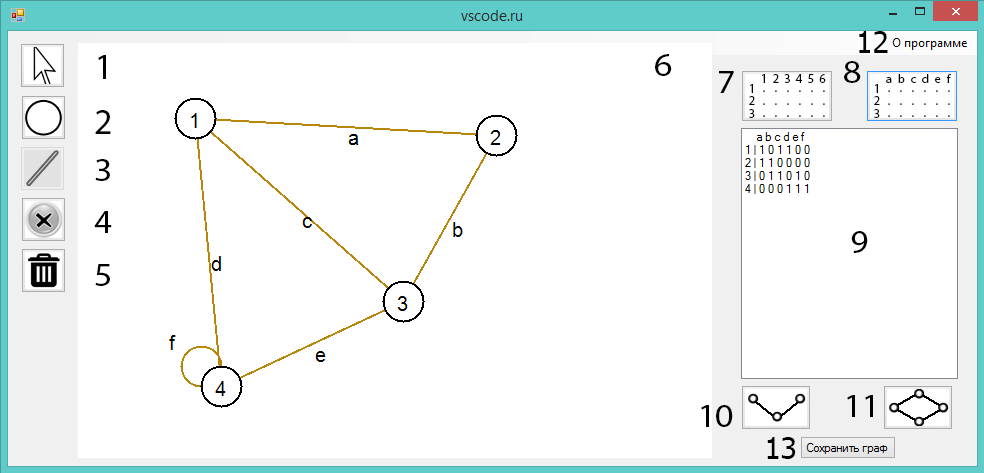
- Алгоритм приближенного последовательного раскрашивания графа Помогите исправить алгоритм что то там не так матрица 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, Алгоритм Дейкстры и цикл for для заполнения веса рёбер графа Здравствуйте, форумчане.
- Так как граф является двудольным тогда и только тогда, когда все циклы четны, определить двудольность можно за один проход в глубину.
- Алгебра приходит на помощь
- В этом уроке мы разберем, что такое раскраска графов и как это относится к цифрам на вершинах. Также покажем примеры раскраски графов разных типов, так как в каждом случае этот процесс немного отличается.
- Ваши алгоритмы не работают на графах с одинаковыми степенями вершин. Собственно успешность алгоритма зависит от того с какой вершины начать.
- Раскраска графа — теоретико-графовая конструкция, частный случай разметки графа. При раскраске элементам графа ставятся в соответствие метки с учётом определённых ограничений; эти метки традиционно называются «цветами».



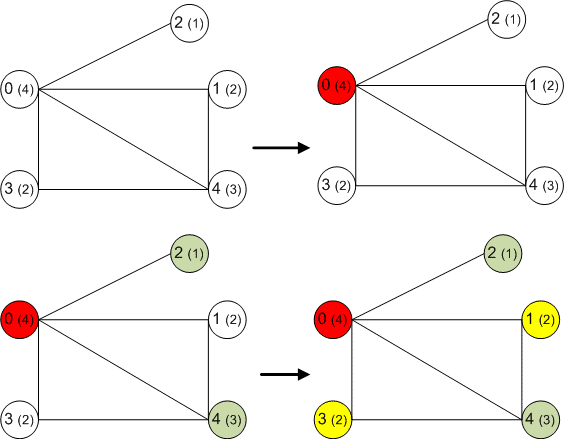

| Алгоритм раскраски графа с перекраской двуцветных компонент | 369 | Другими словами, раскраска задаёт цвет каждой вершине графа. Раскраска называется правильной, если никакие две смежные вершины не окрашены в один цвет. |
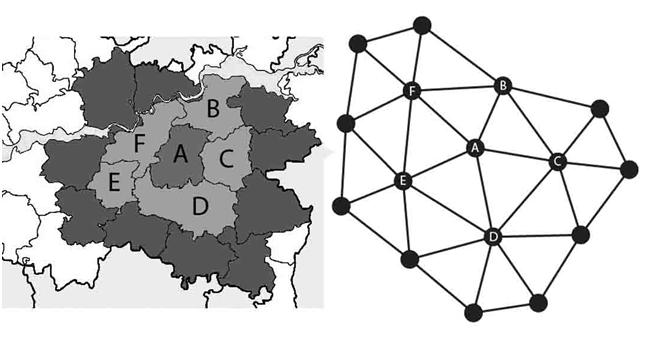
| 358 | Первоначально раскраски графов были нужны для составления географических карт [1]. Сегодня же они в частности раскраска с использованием минимального количества цветов используются, например, для составления расписаний, распределения регистров в микропроцессорах, распараллеливания численных методов. | |
| 456 | Недавно я переписал алгоритм субоптимальной правильной вершинной раскраски графа на Python. Решил выложить его сюда. |
Корректной раскраской графа в два цвета называется такая раскраска, что никакое ребро не соединяет две вершины одного цвета. Графы, которые можно так раскрасить, называют двудольными. Заметим, что если такая раскраска существует, и если зафиксировать цвет одной вершины, то все цвета всех достижимых из неё вершин определяются однозначно: пусть цвет этой вершины белый, тогда все её соседи будут иметь черный цвет, все вершины на расстоянии 2 будут иметь снова белый цвет, все вершины на расстоянии 3 снова черный, и так далее.